Complex eigenvalues of real matrices mean rotations
The real vector space $\mathbb{R}^2$ can be seen as $\mathbb{C}$ in several ways: it depends on what we set as the $i$ (fixed a complex structure $J$, $i$ is identified with $J((1,0)^t)$ and reciprocally, $J$ is determined by the choice of the analogous of $i$). When you have an $\mathbb{R}$-linear operator $A$ in $\mathbb{R}^2$ with complex eigenvalues (that must be conjugate of each other) you can look for the appropriate way of see $\mathbb{R}^2$ as $\mathbb{C}$ in such a manner that $A$ becomes like multiplying by a complex number. Which one? The eigenvalue!! (one of them to your choice). Formally:
Lemma
Let $A$ be a $\mathbb{R}$-linear operator in $\mathbb{R}^2$. If $A$ has two conjugate complex eigenvalues $\lambda$ and $\overline{\lambda}$, then we can find a complex structure in $\mathbb{R}^2$ in such a way that $A$ is like multiplication by $\lambda$ in $\mathbb{C}=\mathbb{R}^2$.
$\blacksquare$
Proof
The complex structure must be a $J$ such that $A=aI+bJ$, where $a+ib$ is an eigenvalue of $A$ with by hypothesis $b\neq 0$. To see that $J^2=-I$ we use the complexification of $\mathbb{R}^2$:
$$ J^{\mathbb{C}}: (\mathbb{R}^2)^{\mathbb{C}} \to (\mathbb{R}^2)^{\mathbb{C}} $$The key is that the map
$$ A^{\mathbb{C}}: (\mathbb{R}^2)^{\mathbb{C}} \to (\mathbb{R}^2)^{\mathbb{C}} $$has the same eigenvalues AND EIGENVECTORS (while $A$ doesn't have the latter ones). Moreover, we can find a basis of eigenvalues in $(\mathbb{R}^2)^{\mathbb{C}}$, say $\{v_1, v_2\}$.Any $w\in(\mathbb{R}^2)^{\mathbb{C}}$ satisfy $w=xv_1+yv_2$. Observe that
$$ A^{\mathbb{C}}(xv_1+yv_2)=x(a+ib)v_1+y(a-ib)v_2 $$so $$ J^{\mathbb{C}}(w)=\frac{1}{b}[A^{\mathbb{C}}-aI^{\mathbb{C}}](w)=\ldots=xiv_1-yiv_2 $$and since
$$ A^{\mathbb{C}}(xiv_1-yiv_2)=\ldots=xiav_1-xbv_1-yaiv_2-ybv_2 $$we get
$$ J^{\mathbb{C}}(J^{\mathbb{C}}(w))=J^{\mathbb{C}}(w)(xiv_1-yiv_2)=\ldots=-w=-I^{\mathbb{C}}(w) $$And since $A^{\mathbb{C}}=B^{\mathbb{C}}$ implies $A=B$, we obtain
$$ J^2=-I $$Therefore, $J$ is a complex structure and
$$A:\mathbb{R}^2_J\mapsto \mathbb{R}^2_J$$
is such that
$$ A(v)=(a+ib)v $$$\blacksquare$
Visually:
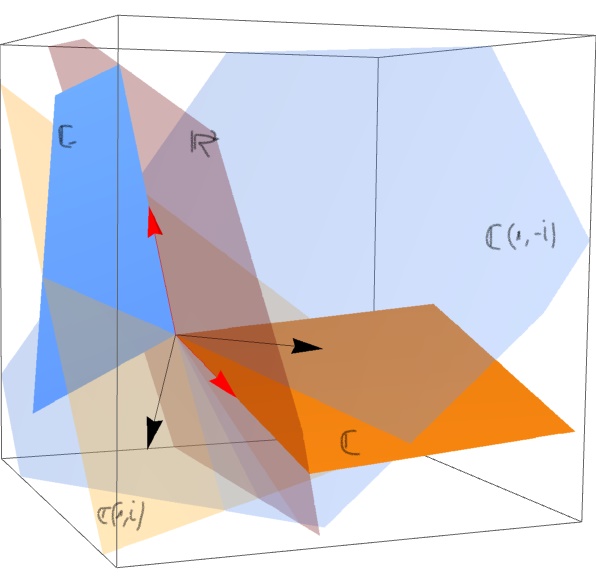
Assume the eigenvalues have module one. In the picture above we see in red the real vector space $\mathbb{R}^2$, with the usual base $e_1, e_2$ in red. If we take the complexified $(\mathbb{R}^2)^{\mathbb{C}}$ we extend $e_1$ and $e_2$ not as a line, but each one as a plane $\mathbb{C}$ (the solid orange plane and the blue one). The whole system is a four dimensional real space (two dimensional complex space), the complex plane $\mathbb C^2$. The map $A$ has eigenvectors $v_1$ and $v_2$ (the black ones in the picture). When we apply $A$ this eigenvectors rotate inside their complex line $\mathbb{C} v_1$ y $\mathbb{C} v_2$ (the yellow and the blue transparent planes in the picture). This rotations (one of angle $\theta$ and other of $-\theta$ since they are conjugates eigenvalues) compensate'' each other in such a way that they produce a rotation in the original real plane $\mathbb{R}^2$ (the transparent red one).
This rotation of the original plane induces a complex structure in $\mathbb{R}^2$ which is, in some sense, _transversal_: the red transparent plane is not a complex line, so it has no natural complex structure...
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: